-
Boundedness of Littlewood-Paley Operators in Variable Morrey Spaces
Panwang Wang,
Zongguang Liu
Issue:
Volume 10, Issue 2, April 2022
Pages:
15-28
Received:
14 February 2022
Accepted:
7 March 2022
Published:
17 March 2022
Abstract: In this paper, the authors prove norm inequalities for the intrinsic square functions and commutators generated by this class operator and BMO function in variable Morrey spaces. This implies that the same norm inequalities for the Lusin area integrals, the Littlewood-Paley operators and the continuous square functions. As application, we get the boundedness for convolution Calderón-Zygmund operators in generalized Morrey spaces.
Abstract: In this paper, the authors prove norm inequalities for the intrinsic square functions and commutators generated by this class operator and BMO function in variable Morrey spaces. This implies that the same norm inequalities for the Lusin area integrals, the Littlewood-Paley operators and the continuous square functions. As application, we get the b...
Show More
-
On MHD Flow of Non-newtonian Viscoelastic Fluid over a Stretched Magnetized Surface
Golbert Aloliga,
Ibrahim Yakubu Seini,
Rabiu Musah
Issue:
Volume 10, Issue 2, April 2022
Pages:
29-42
Received:
14 March 2022
Accepted:
1 April 2022
Published:
9 April 2022
Abstract: The purpose of this research is to investigate heat and mass transport in a magnetohydrodynamic (MHD) flow of a non-Newtonian viscoelastic fluid on a stretched magnetized surface. The investigations involve modelling the governing partial differential equations with respect to the Cartesian coordinate system. The models are then transformed into a set of coupled ordinary differential equations. Numerical and graphical solutions were obtained using similarity analysis. The effect of the magnetized sheet on the flow behavior; local skin friction, Nusselt, and Sherwood numbers, are presented in tables. It was observed that an enhanced thickening of the thermal boundary layer was due to the induced magnetization of the sheet. This leads to a significant decline in the heat transfer rate. Certain significant discoveries reported in this research discloses that the effect of viscous dissipation and the non-uniform heat transmission have momentous impact in controlling the rate of heat transfer in the boundary layer region. Again, from the outcome of the analysis it is seen that, the effect of appreciating the Soret number or lessening the Dufour number tends to decrease the velocity and temperature profiles while enhancing the concentration dissemination. Magnetizing the surface shows similar effects on the local skin friction, Nusselt number, and Sherwood number. It is concluded that magnetized surfaces significantly influence the rate of cooling and hence the quality of the penultimate product.
Abstract: The purpose of this research is to investigate heat and mass transport in a magnetohydrodynamic (MHD) flow of a non-Newtonian viscoelastic fluid on a stretched magnetized surface. The investigations involve modelling the governing partial differential equations with respect to the Cartesian coordinate system. The models are then transformed into a ...
Show More
-
Connectedness Generalizations Using the Concept of Adherence Dominators
James Edward Joseph,
Bhamini M. P. Nayar
Issue:
Volume 10, Issue 2, April 2022
Pages:
43-50
Received:
6 March 2022
Accepted:
30 March 2022
Published:
23 April 2022
Abstract: An adherence dominator on a topological space X is a function π from the collection of filterbases on X to the collection of closed subsets of X satisfying 
Ω ⊂ πΩ where Ω is the adherence of Ω and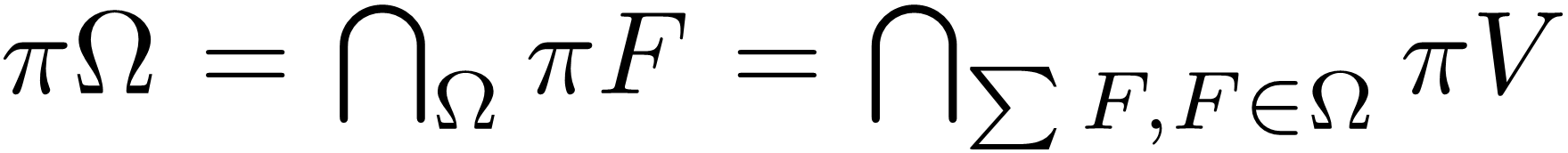 
, where ∑F represents the collection of open sets containing F. The π-adherence may be adherence, θ-adherence, u-adherence s-adherence, f-adherence, δ-adherence, etc., of a filterbase. Pervin deined a partition (or a separation) of a set in a topological space as a pair of subsets (P,Q) satisfying P∩clQ = clP∩Q = ∅, where clP represents the closure of P and a set K is said to be connected if K = ∅ or K ≠ P
Q where (P,Q) is a partition. In this paper, a πpartition (or a πseparation) is a pair of subsets (P,Q) satisfying P∩πQ = πP∩Q = ∅ where π is an adherence dominator and a subset K of a space X is πconnected relative to X lf K = ∅ or there is no πpartition (P,Q) such that K = PQ. This paper investigates these new forms of connectedness. Theorems due to A. D. Wallace and J. D. Kline are generalized. Geralizations of C-compact spaces and functionally compact spaces are also presented.
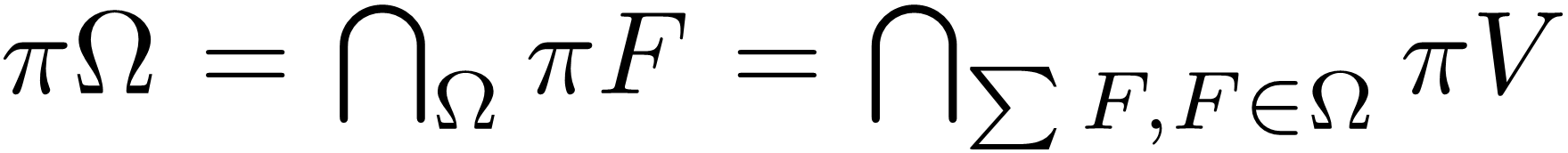Abstract: An adherence dominator on a topological space X is a function π from the collection of filterbases on X to the collection of closed subsets of X satisfying Ω ⊂ πΩ where Ω is the adherence of Ω and , where ∑F represents the collection of open sets containing F. The π-adherence may be adherence, θ-adherence, u-adherence s-adherence, f-adherence, δ-ad...
Show More
-
Locally H-closed Spaces, Subspaces and Their Extensions
James Edward Joseph,
Bhamini M. P. Nayar
Issue:
Volume 10, Issue 2, April 2022
Pages:
51-58
Received:
7 March 2022
Accepted:
11 April 2022
Published:
23 April 2022
Abstract: The primary goal is to characterize Locally H-closed spaces (LHC), by conditions on the remainders of their extensions. These spaces are also characterized using subspaces and their extensions as well. Characterizing these classes of spaces using the remainders of the subspaces in their extensions provide characterizations of them in terms of their boundaries. Recently, the authors have proved that these results give necessary and sufficient conditions for the space to be compact A number of equivalences are proved for Hausdorff (Urysohn) [regular] spaces. These results lead to similar characterizations of Locally Urysohn-closed (LUC) as well as Locally regular-closed (LRC) spaces. Some of these equivalent properties generalize a number of existing results on these topics. In the present article it is shown that if X is a Hausdorff LHC space then each closed set is an intersection of regularly open sets as well as each closed set is an intersection of semi-closed neighborhoods. In 1969 Porter and Thomas had shown that in a Hausdorff space a locally H-closed subspace is the intersection of an open set and a closed set. In this article, it is shown that a space X is LHC if and only if every nonempty proper regularly closed subset of X is LHC.
Abstract: The primary goal is to characterize Locally H-closed spaces (LHC), by conditions on the remainders of their extensions. These spaces are also characterized using subspaces and their extensions as well. Characterizing these classes of spaces using the remainders of the subspaces in their extensions provide characterizations of them in terms of their...
Show More
-
Interval Estimation of the Absolute Risk of an Event with Competing Risks Using Proportional Regression of Cause-Specific Hazards
Michael Richard Crager,
Jerome Victor Braun
Issue:
Volume 10, Issue 2, April 2022
Pages:
59-85
Received:
4 April 2022
Accepted:
19 April 2022
Published:
28 April 2022
Abstract: It is often important to account for the effects of a competing risk when estimating the risk of a particular event of interest by estimating its absolute risk. Available methodology for interval estimation of the absolute risk using the proportional regression of cause-specific hazards (CSH) has been limited to situations with time-invariant covariates and a single random censoring mechanism, without accommodation of cohort sampling study designs. Here we derive asymptotic pointwise confidence intervals in closed form for the absolute risk of an event at a specified time (the value of the cumulative incidence function) in the presence of competing risks using proportional CSH regression, accommodating external time-dependent covariates, cohort sampling study designs and multiple censoring mechanisms. Different covariates may be used for the event of interest and the various competing risks. Consistent with the definition of absolute risk, the CSH method produces absolute risk estimates that are less than or approximately equal to corresponding “conditional” risk estimates that do not account for competing risks. An example shows that this property is not necessarily shared by methods based on subdistribution hazard regression. Simulation studies indicate that the CSH method confidence intervals computed on the log cumulative hazard or the risk scale have coverage probabilities that approximate the nominal level for small and moderate samples, provided that the number of events per covariate is at least 10 and, when using cohort sampling, the ratio of patients without events to patients with events is at least 2:1.
Abstract: It is often important to account for the effects of a competing risk when estimating the risk of a particular event of interest by estimating its absolute risk. Available methodology for interval estimation of the absolute risk using the proportional regression of cause-specific hazards (CSH) has been limited to situations with time-invariant covar...
Show More
